梯度下降法 BGD、SGD、MBGD
梯度下降法的计算过程就是沿梯度下降的方向求解极小值,重复地计算梯度然后对参数进行更新,这一过程称为梯度下降.
假设线性回归函数为:
\[\begin{align*} h_{\theta} = \sum_{j=0}^{n} \theta_{j} x_{j} = \theta^T x \end{align*}\]其损失函数为:
\[\begin{align*} J_{train}(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^{2} \end{align*}\]一阶导数表示为
\[\nabla_{\theta}J = \frac{\partial J}{\partial \theta}\]某二维参数组($\theta_{0}$ 和 $\theta_{1}$)对应损失函数可视化图为:
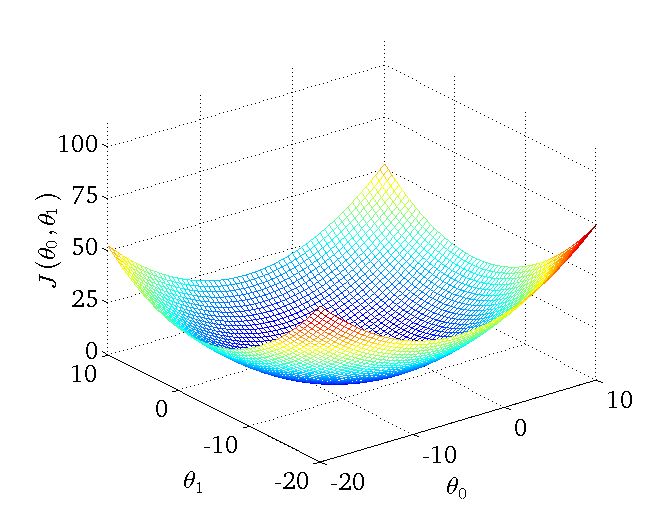
批量梯度下降法(Batch Gradient Descent,BGD)
梯度下降的最原始的形式,按照每个参数$\theta$的梯度负方向更新每个参数$\theta$:
\[\begin{align*} \theta_j' & = \theta_j-\eta\nabla_{\theta}J(\theta) \\ & = \theta_j- \eta\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)} \end{align*}\]其中,$\eta$表示 学习率 (Learning Rate).最终得到的是一个全局最优解,但是每迭代一步,都要用到训练集所有的数据,如果样本数目很大,那么这种方法的迭代速度会很慢.
其中求偏导数过程为
\[\begin{align*} \nabla_{\theta}J(\theta) & = \frac{\partial J(\theta)}{\partial \theta_j} \\ & = \frac{\partial}{\partial \theta_j} \frac{1}{2m} (h_{\theta}(x^{(i)})-y^{(i)})^2 \\ & = 2\cdot\frac{1}{2m}(h_{\theta}(x^{(i)})-y^{(i)})\cdot\frac{\partial}{\partial \theta_j}(h_{\theta}(x^{(i)})-y^{(i)}) \\ & = \frac{1}{m}(h_{\theta}(x^{(i)})-y^{(i)})\cdot\frac{\partial}{\partial \theta_j}(\sum_{j=0}^n\theta_jx_j^{(i)}-y^{(i)}) \\ & = \frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)} \end{align*}\]优点:全局最优解;易于并行实现;
缺点:样本数目过多,训练过程会很慢.
从迭代的次数上来看,BGD迭代的次数相对较少.其迭代的收敛曲线示意图可以表示如下:
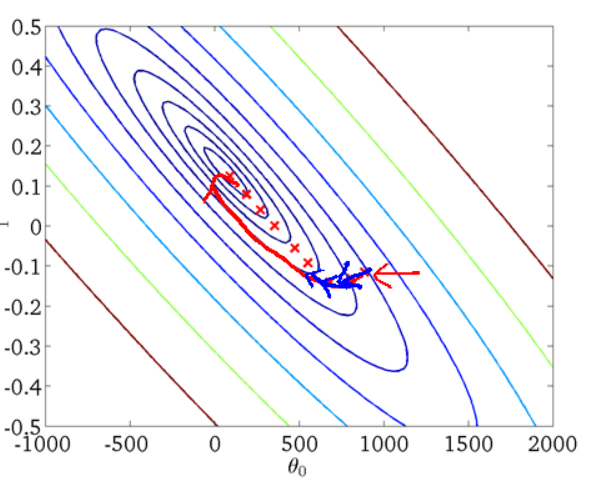
随机梯度下降法(Stochastic Gradient Descent,SGD)
解决BGD在大规模下速度减慢的问题,数学形式如下:
(1)损失函数表示为
\[\begin{align*} J(\theta) & = \frac{1}{m}\sum_{i=1}^{m}\frac{1}{2}(y^{(i)}-h_{\theta}(x^{(i)}))^2 \\ & = \frac{1}{m}\sum_{i=1}^{m}cost(\theta,(x^{(i)},y^{(i)})) \end{align*} \\ cost(\theta,(x^{(i)},y^{(i)}))=\frac{1}{2}(y^{(i)}-h_{\theta}(x^{(i)}))^2\](2)利用每个样本的损失函数$cost(\theta,(x^{(i)},y^{(i)}))$对$\theta$求偏导得到对应梯度来更新$\theta$,即
\[\begin{align*} \theta' & = \theta-\eta\nabla_{\theta}J(\theta,(x^{(i)},y^{(i)})) \\ & = \theta+(y^{(i)}-h_{\theta}(x^{(i)}))x_j^{(i)} \end{align*}\]其中,$\eta$表示 学习率 (Learning Rate)
随机梯度下降是通过每个样本来迭代更新一次,如果样本量很大的情况(例如几十万),那么可能只用其中几万条或者几千条的样本,就已经将$\theta$迭代到最优解了,对比上面的批量梯度下降,迭代一次需要用到十几万训练样本,一次迭代不可能最优,如果迭代10次的话就需要遍历训练样本10次.但是,SGD伴随的一个问题是噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向.
优点:训练速度快;
缺点:
- 选择合适的learning rate比较困难;
- 对所有的参数更新使用同样的learning rate.对于稀疏数据或者特征,有时我们可能想更新快一些对于不经常出现的特征,对于常出现的特征更新慢一些,这时候SGD就不太能满足要求了;
- SGD容易收敛到局部最优,并且容易被困在鞍点,准确度下降;
- 不易并行实现.
从迭代的次数上来看,SGD迭代的次数较多,在解空间的搜索过程看起来很盲目.其迭代的收敛曲线示意图可以表示如下:
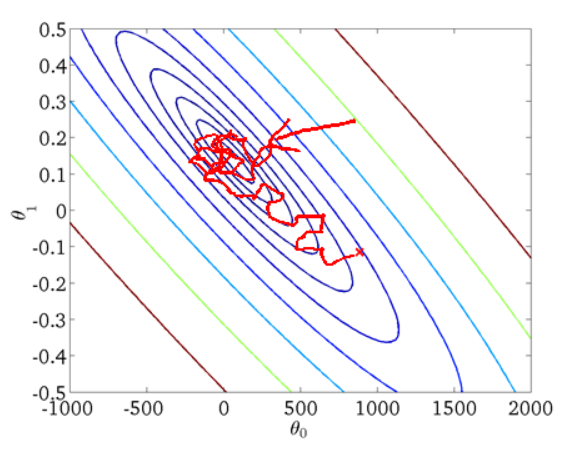
小批量/批梯度下降法(Mini-atch Gradient Descent,MBGD)
MBGD是BGD和SGD的折衷,MBGD在每次更新参数时使用$n$个样本,迭代公式为:
\[\begin{align*} \theta'=\theta-\eta\nabla_{\theta}J(\theta,(x^{(i:i+n)},y^{(i:i+n)}) \end{align*}\]其中,$\eta$表示 学习率 (Learning Rate),$n$表示 批尺寸(Batch size)
Momentum
momentum是模拟物理里动量的概念.它在相关方向加速SGD,抑制振荡,从而加快收敛 在梯度指向同一方向的维度,momentum项增加;在梯度改变方向的维度,momentum项减少更新.
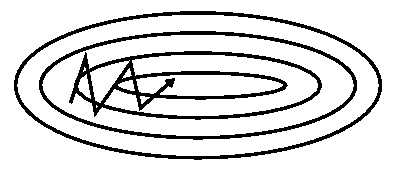
不加momentum项的SGD
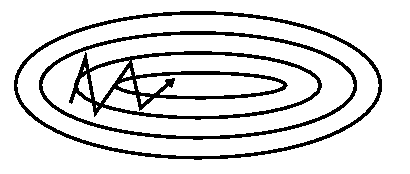
带momentum项的SGD
Nesterov
nesterov项在梯度更新时做一个校正,避免前进太快,同时提高灵敏度.
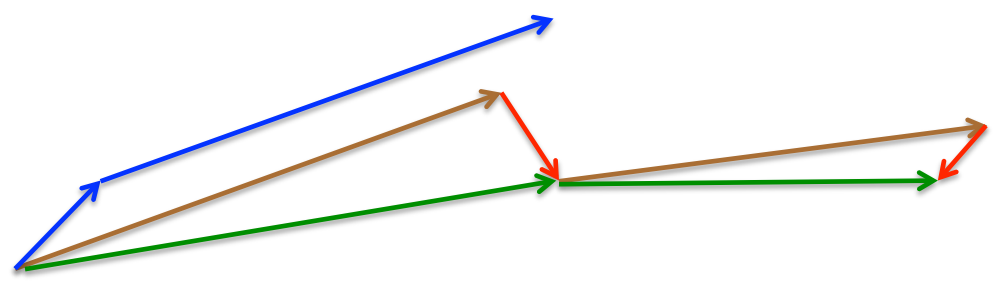
momentum首先计算一个梯度(短的蓝色向量),然后在加速更新梯度的方向进行一个大的跳跃(长的蓝色向量),nesterov项首先在之前加速的梯度方向进行一个大的跳跃(棕色向量),计算梯度然后进行校正(绿色梯向量).
其实,momentum项和nesterov项都是为了使梯度更新更加灵活,有不同情况有针对性.但是,人工设置一些学习率总还是有些生硬,接下来介绍几种自适应学习率的方法.
Adagrad
此方法能对不常见的参数进行较大的更新,对于常见参数更新较小,不用手动调节学习率.
缺点:因为公式中分母上会累加梯度平方,这样在训练中持续增大的话,会使学习率非常小,甚至趋近无穷小.
Adadelta
Adadelta是对Adagrad的扩展.Adagrad会累加之前所有的梯度平方,而Adadelta只累加固定大小的项,并且也不直接存储这些项,仅仅是计算对应的平均值.Adadelta甚至不用设置默认值.
RMSprop
RMSprop类似于Adadelta.
Adam(Adaptive Moment Estimation)
Adam加上了bias校正和momentum,在优化末期,梯度更稀疏时,它比RMSprop稍微好点.
总结
Batch gradient descent: Use all examples in each iteration;
Stochastic gradient descent: Use 1 example in each iteration;
Mini-batch gradient descent: Use b examples in each iteration.
对于稀疏数据,尽量使用学习率可自适应的优化方法,不用手动调节,而且最好采用默认值 SGD通常训练时间更长,容易陷入鞍点,但是在好的初始化和学习率调度方案的情况下,结果更可靠 如果在意更快的收敛,并且需要训练较深较复杂的网络时,推荐使用学习率自适应的优化方法. Adadelta,RMSprop,Adam是比较相近的算法,在相似的情况下表现差不多.
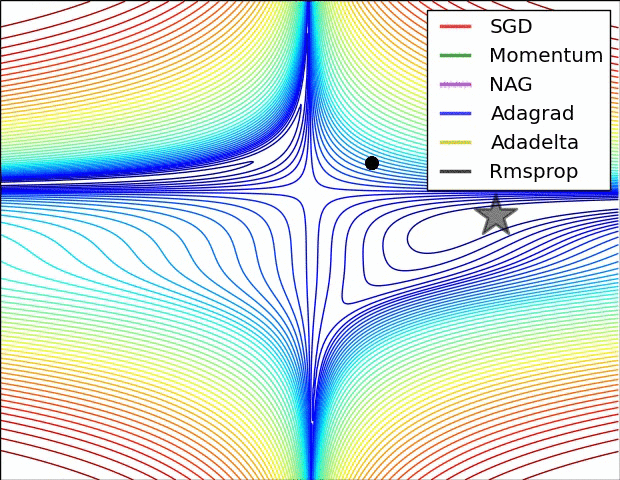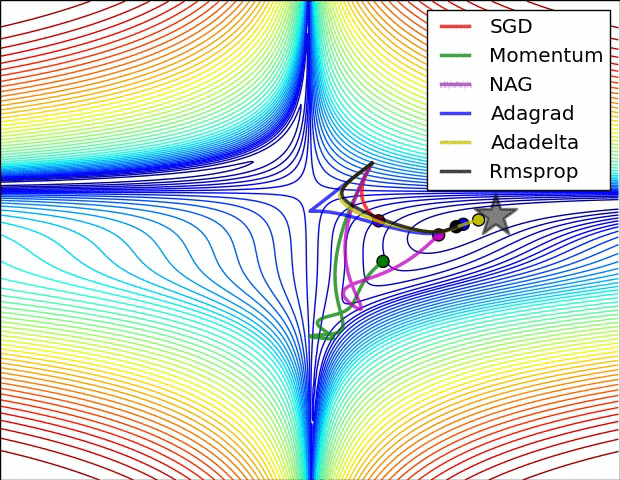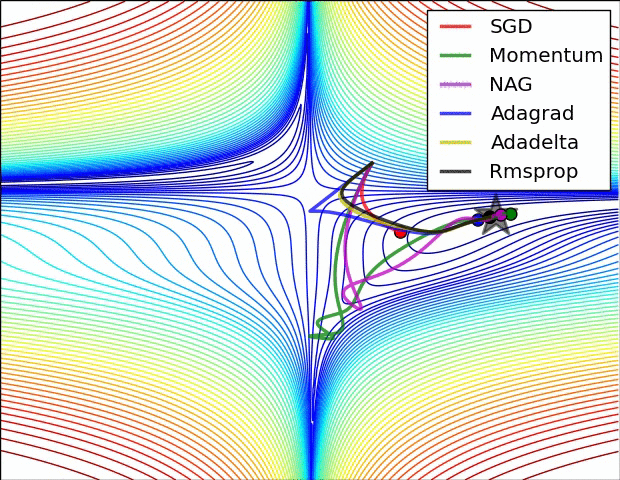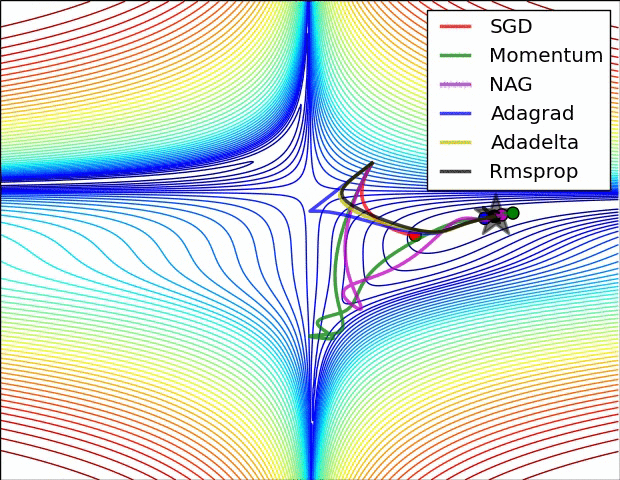
损失平面等高线
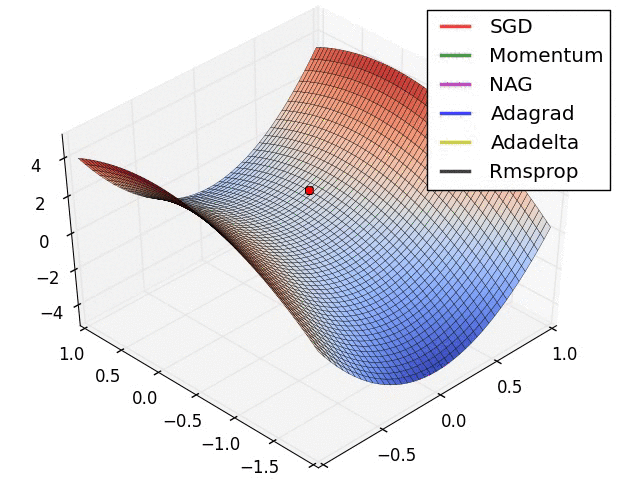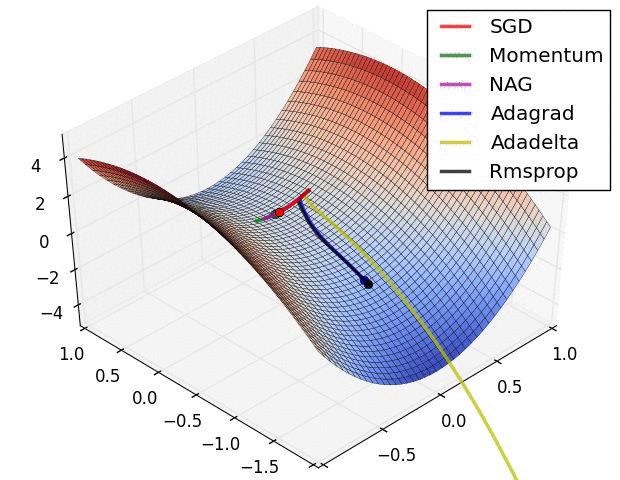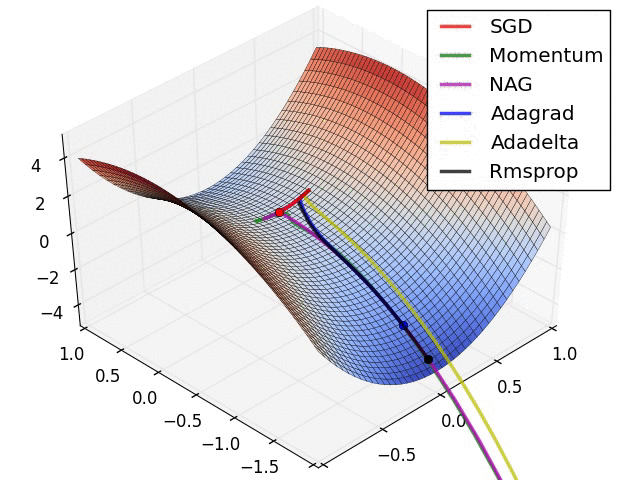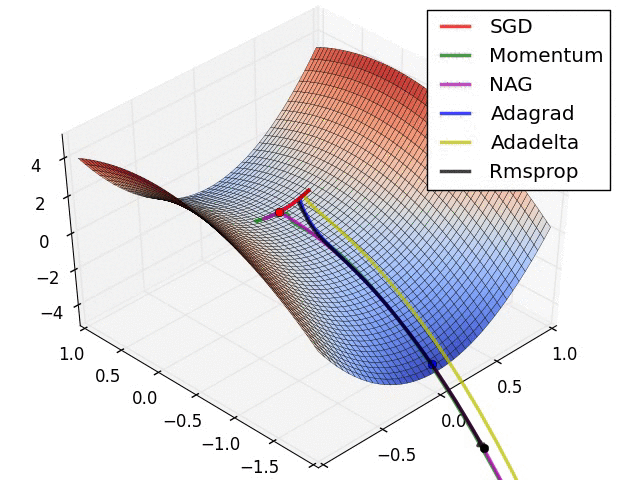
在鞍点处的比较
参考
[Machine Learning] 梯度下降法的三种形式BGD、SGD以及MBGD
An overview of gradient descent optimization algorithms
An overview of gradient descent optimization algorithms(arXiv)